First we find the area of the first park

area is 6300 square meters
now find the perimeter
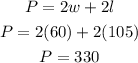
perimeter is 330 meters
now we need to write equations to find the measures of the another park and we can write from the statements
has the same perimeter
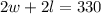
but a smaller area
then we choose an area smaller than 6300, for example 6000
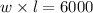
now we have two equations and two unknows
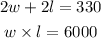
then we can solve a unknow from one equation and replace on the other
I will solve w from the first equation and replace on second

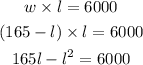
rewrite the equation
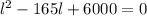
and use quadratic formula to solve L
![\begin{gathered} l=\frac{-b\pm\sqrt[]{b^2-4ac}}{2a} \\ \\ l=\frac{-(-165)\pm\sqrt[]{(-165)^2-4(1)(6000)}}{2(1)} \\ \\ l=\frac{165\pm\sqrt[]{27225-24000}}{2} \\ \\ l=\frac{165\pm\sqrt[]{3225}}{2} \end{gathered}](https://img.qammunity.org/qa-images/2023/formulas/mathematics/college/jn0dpmw893p7a9y956o3.png)
then we have two values for l
![\begin{gathered} l_1=\frac{165+\sqrt[]{3225}}{2}=110.9 \\ \\ l_2=\frac{165-\sqrt[]{3225}}{2}=54.1 \end{gathered}](https://img.qammunity.org/qa-images/2023/formulas/mathematics/college/odrdeevx6uv4vqtx6b3o.png)
we can take any value because both are positive and replace on any equation to find w
I will replace l=110.9 to find w
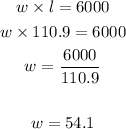
Finally the length and wifth of the other rectangle patks are
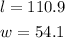
meters