Question

The half-life of a certain substance is 27 years. How long will it take for a sample of this substance to decay to 66% of its original amount? for the sample of the substance to decay to 66% of its original amount

Answer 1

This is a type of radioactive decay problem. Given an initial amount of N0, the amount at t years is given by

`N(t)=N_0e^(-\lambda t)`

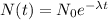
The information "27 years is the half-life of the substance" means that if we replace t by 27, we will get exactly half of the initial amount we had. That is

`N_0e^(-\lambda\cdot27)=(N_0)/(2)`

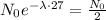
We can cancell out N0 on both sides, so we get

`e^(-\lambda\cdot27)=(1)/(2)`

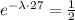
using the properties of exponentials, we have the equivalent equation

`(1)/(2)=(1)/(e^(\lambda\cdot27))`

which is also equivalent to

`e^(\lambda\cdot27)=2`

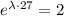
If we apply natural logarithm on both sides, we get

`\ln (e^(\lambda\cdot27))=\lambda\cdot27=\ln (2)`

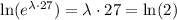
Finally, we can divide both sides by 27, to get

`\lambda=(\ln (2))/(27)`

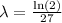
So, the function that describes the amount of the subtances at time t is given as

`N(t)=N_0e^{(-\ln (2)\cdot t)/(27)}`

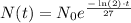
Now, we want to calculate the value of t, for which the amount we have at year t is exactly 66% of what we have at t=0. That is

`\frac{N_0e^{-(\ln (2)\cdot t)/(27)}}{N_0}=0.66`

We can cancell out N0 and, by equivalence by using the properties of exponents, we get

`\frac{1}{e^{(\ln(2))/(27)\cdot t}}=0.66`

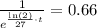
which is also equivalent to

`(1)/(0.66)=e^{(\ln (2)t)/(27)}`

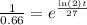
if we apply the natural logarithm on both sides, we get

`\ln ((1)/(0.66))=\ln (e^{(\ln(2)\cdot t)/(27)})=\ln (2)\cdot(t)/(27)`

Finally, we want to solve for t. To do so, we can multiply by 27 and then divide by ln(2). So we get

`t=(27)/(\ln(2))\cdot\ln ((1)/(0.66))`

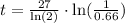
with help of a calculator, we have that t is approximately 16.185. That is, about after 16 years, we will have 66% of the initial amount.