Question

Use the Distance and Slope Formulas to complete the tables below. Round to the nearest tenth,1. Find the length of MN, given the coordinates M (4,- 4) and N (2.0).imImMN:

Answer 1

Given the coordinates;

`\begin{gathered} M(4,-4) \\ N(2,0) \end{gathered}`

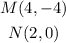
The slope m of the line MN is;

`\begin{gathered} m=(y_2-y_1)/(x_2-x_1) \\ \text{Where x}_1=4,y_1=-4,x_2=2,y_2=0 \end{gathered}`
`\begin{gathered} m=(0-(-4))/(2-4) \\ m=(4)/(-2) \\ m=-2 \end{gathered}`

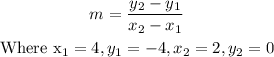
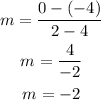
The slope of a line parallel to the line MN must have a slope equal to line MN, that is;

`\mleft\Vert m=-2\mright?`

The slope of a line perpendicular to line MN has a slope of negative reciprocal of line MN, that is;

`\begin{gathered} \perp m=-(1)/(-2) \\ \perp m=(1)/(2) \end{gathered}`

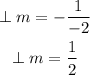
Using the distance formula to find the length of MN, the formula is given as;

`D=\sqrt[]{(y_2-y_1)^2+(x_2-x_1)^2}`
`\begin{gathered} \text{Where x}_1=4,y_1=-4,x_2=2,y_2=0 \\ |MN|=\sqrt[]{(0-(-4)^2+(2-4)^2} \\ |MN|=\sqrt[]{16+4} \\ |MN|=\sqrt[]{20} \\ |MN|=4.5 \end{gathered}`