Question

The volume of an iceberg that is below the water line is 2^5 cubic meters. the volume that is above the water line is 2^2 cubic meters. how many times greater is the volume below the water line than above it?

Answer 1

Let:

`\begin{gathered} V_1\colon\text{ volume of iceberg below the water line} \\ V_2\colon\text{ volume of iceberg above the waterline} \end{gathered}`

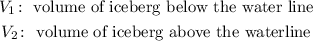
We want to finde some number k such that we can express the volume of the iceberg below the water line as the product of k and the volume of the iceberg above the waterline, this is:

`V_1=k\cdot V_2`

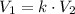
then, solving for k we have the following:

`\begin{gathered} V_1=2^5m^3 \\ V_2=2^2m^3 \\ V_1=k\cdot V_2 \\ \Rightarrow k=(V_1)/(V_2)=(2^5)/(2^2)=2^(5-2)=2^3^{} \\ k=2^3 \end{gathered}`

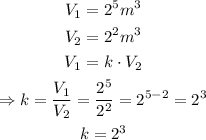
we have that k=2^3. This means that the volume of the iceberg above the water line is 2^3 times the volume of the iceberg below the water line