Question

5. How much must be deposited now at 5% compounded semi-annually to yield an annuity payment of ₱30,000 at the beginning of each 6-month period for 6 years?

Answer 1

Given the question in the question tab, the following are the solution steps to calculate the amount to be deposited

STEP 1: Write the formula for Future value annuity

`FV=P*((1+r)^n-1)/(r)`

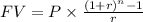
Where:

FV = present value of an ordinary annuity

P=value of each payment

r=interest rate per period

n=number of periods

STEP 2: Write the given parameters

`\begin{gathered} FV=30000,r=5,n=12,r=(5)/(100)=0.05,P=? \\ n=12\text{ because }6\text{months period for 6 years will be 2}*6=12 \end{gathered}`

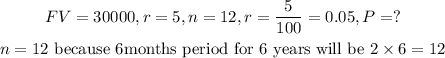
STEP 3: Calculate the P

`\begin{gathered} FV=P*((1+r)^n-1)/(r) \\ 30000=P*((1+0.05)^(12)-1)/(0.05) \\ 30000=P*((1.05)^(12)-1)/(0.05) \\ 30000=P*((1.05)^(12)-1)/(0.05) \\ 30000=P*\frac{1.795856326^{}-1}{0.05} \\ 30000=P*\frac{0.795856326^{}}{0.05} \\ 30000=\frac{0.795856326P^{}}{0.05} \\ By\text{ cross multiplication,} \\ 30000*0.05=0.795856326P \\ 1500=0.795856326P \\ (0.795856326P)/(0.795856326)=(1500)/(0.795856326) \\ P=1884.762301 \\ P\approx1884.76 \end{gathered}`

Hence, the amount that must be deposited now is approximately 1884.76 to the nearest cents