Question

A beaker of mass 1.2 kg containing 2.5 kg of water rests on a scale. A 3.8 kg block of a metallic alloy of density 3300 kg/m3 is suspended from a spring scale and is submerged in the water of density 1000 kg/m? as shown in the figure. a) What does the hanging scale read? acceleration of gravity is 9.8 m/s?Answer in units of N.b) what does the lower scale read? Answer in units of N.

Answer 1

a) 25.97 N

b) 47.53 N

Explanation:

Given:

Beaker mass = 1.2 kg

Water mass = 2.5 kg

Water density = 1000 kg/m^3

Block mass = 3.8 kg

Block density = 3300 kg/m^3

a)

The first thing is to calculate the volume of the block, like this:

`\begin{gathered} d=(m)/(V) \\ V=(m)/(d) \\ \text{ we replacing} \\ V=(3.8)/(3300) \\ V=0.00115m^3 \end{gathered}`

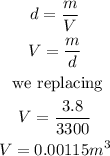
Mass of water displaced by the block is:

`\begin{gathered} d=(m)/(V) \\ m=d\cdot V \\ m=1000\cdot0.00115 \\ m=1.15kg \end{gathered}`

The block will receive a push from the water equal to the weight of the water displaced by the block, or the effective weight of the block will be reduced by the same amount:

`\begin{gathered} W=(m_b-m)\cdot g \\ \text{ we replacing} \\ W=(3.8-1.15)\cdot9.8 \\ W=25.97\text{ N} \end{gathered}`

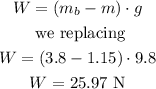
Therefore, 25.97 N is the reading on the hanging scale.

b)

The bottom scale will gain by the same amount (1.15 kg). Therefore, the totalweight on the bottom scale is:

`\begin{gathered} W=(1.2+2.5+1.15)\cdot9.8 \\ W=4.85\cdot9.8 \\ W=47.53\text{ N} \end{gathered}`

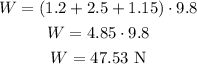
Therefore, 47.53 N is the reading on the lower scale.