Question

Write the equation in standard form for the circle passing through (-7,7) centered at theorigin.

Answer 1

Step 1

State the equation of a circle

`(x-h)^2+(y-k)^2=r^2`

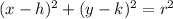
Where

h= -7

k= 7

Step 2

Find r

r is the distance between the origin and (-7,7)

Distance between 2 points is

`d=\sqrt[]{(x_2-x_1)^2+(y_2-y_1)^2^{}}`
`\begin{gathered} \text{where} \\ x_2=0 \\ x_1=-7 \\ y_2=0 \\ y_1=7 \end{gathered}`

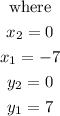
Hence the distance is given as

`\begin{gathered} d=\sqrt[]{(0-(-7))^2+(0-7)^2} \\ d\text{ =}\sqrt[]{49+49} \\ d=\sqrt[]{98} \\ d=7\sqrt[]{2} \end{gathered}`

Hence r =7√2

Step 3

Write the equation in standard form after substitution.

`\begin{gathered} (x-(-7))^2+(y-7)^2=(7\sqrt[]{2})^2 \\ (x+7)^2+(y-7)^2=(7\sqrt[]{2})^2 \end{gathered}`