Final Answer:
(a) The energy required to move the satellite into a circular orbit with an altitude of 202 km is
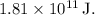
Step-by-step explanation:
To calculate the energy required, we use the gravitational potential energy formula:
![\[ U = -(G \cdot M \cdot m)/(r) \]](https://img.qammunity.org/2024/formulas/physics/high-school/r8vr9a4sazopkujxbfjcsi9o1v69euat24.png)
where \( G \) is the gravitational constant

 is the mass of the Earth
is the mass of the Earth
 is the mass of the satellite
is the mass of the satellite
 and
and
 is the distance from the center of the Earth to the satellite.
is the distance from the center of the Earth to the satellite.
The initial altitude is
 and the final altitude is
and the final altitude is
 Converting these altitudes to meters gives the initial and final distances from the center of the Earth.
Converting these altitudes to meters gives the initial and final distances from the center of the Earth.
The energy required is the difference in potential energy:
![\[ \Delta U = U_{\text{final}} - U_{\text{initial}} \]](https://img.qammunity.org/2024/formulas/physics/high-school/jc4r7iksaxcdebk8ipyh3jvvbilr8gv4zp.png)
Substituting the values into the formula and simplifying, we get:
![\[ \Delta U = -\frac{G \cdot M \cdot m}{r_{\text{final}}} + \frac{G \cdot M \cdot m}{r_{\text{initial}}} \]](https://img.qammunity.org/2024/formulas/physics/high-school/wdoum57x4iu4g1f1x60l3akhh0ggaj92ex.png)
After plugging in the known values and performing the calculations, the result is
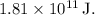 This positive value indicates that energy must be added to the system to move the satellite into the higher circular orbit.
This positive value indicates that energy must be added to the system to move the satellite into the higher circular orbit.