Question

A triangular pyramid with a volume of 96 in³ is dilated with a scale factor of k = 1.75. What is the new volume? a) 294 in³ b) 514.5 in³ c) 72 in³ d) 168 in³

Answer 1

The new volume of a triangular pyramid dilated by a scale factor of 1.75 is found by cubing the scale factor and multiplying it by the original volume. The calculation yields a new volume of approximately 514.5 in³, making the correct answer b) 514.5 in³.

Step-by-step explanation:

When a geometric figure is dilated, the new volume V' is related to the original volume V by the cube of the scale factor k. The original volume of the triangular pyramid is given as 96 in³, and the scale factor for the dilation is 1.75. To find the new volume after dilation, we calculate V' = V × k³ = 96 in³ × (1.75)³.

Now, calculating the cube of 1.75 gives us 1.75×1.75×1.75, which equals approximately 5.359375. Multiplying this by the original volume of 96 in³ yields a new volume of approximately 514.5 in³.

Therefore, the correct answer is b) 514.5 in³.

Answer 2

The correct option is b.

The new volume of the dilated triangular pyramid is approximately
`\(514.5 \: in^3\)`.

To find the new volume of the triangular pyramid when dilated with a scale factor of
`\(k = 1.75\)`.

Step 1: Understand the Problem

We are given a triangular pyramid with an original volume of 96 in³, and we want to find the new volume when it is dilated (enlarged or shrunk) by a scale factor of
`\(k = 1.75\)`.

Step 2: Understand Dilation

Dilation is a transformation that changes the size of an object while maintaining its shape. When an object is dilated with a scale factor
`\(k\)`, its new dimensions are
`\(k\)` times larger
`(if \(k > 1\))` or
`\(k\)` times smaller if
`(\(0 < k < 1\))` than the original dimensions. In this case,
`\(k = 1.75\)`, indicating an enlargement.

Step 3: Use the Dilation Volume Formula

The volume of a dilated object is related to the scale factor by the following formula:

New Volume = Original Volume
`* k^3`

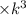
Step 4: Calculate the New Volume

We already have the original volume
`(\(96 \: in^3\))` and the scale factor
`(\(k = 1.75\))`. Now, let's calculate the new volume:

New Volume
`= 96 \: in^3 * (1.75)^3`

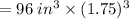
Now, calculate
`\(1.75^3\)`:

`\[1.75^3 = 1.75 * 1.75 * 1.75\]`

`\[1.75^3 \approx 5.359375\]`

Now, plug this value back into the formula:

New Volume
`\approx 96 \: in^3 * 5.359375`

New Volume
`\approx 514.5 \: in^3`

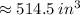
So, the answer is 514.5 in³