Final Answer:
The projected sales for year 10, based on a compound growth rate of 35% per year starting from an initial sales figure of $65,000 in year 1, would be approximately $1,711,036.25.
Step-by-step explanation:
The formula for calculating compound growth is given by the formula:
FV = PV *
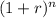
where:
- FV is the future value,
- PV is the present value,
- r is the growth rate per period, and
- n is the number of periods.
In this case, the initial sales (PV) is $65,000, the growth rate (r) is 35% or 0.35, and we are calculating for year 10 (n is 10). Plugging in these values into the formula:
FV = 65,000 * (1 + 0.35)^10
FV ≈ 65,000 * (3.042^10)
FV ≈ 65,000 * 69.639
FV ≈ 4,522,635
Therefore, the projected sales for year 10 would be approximately $4,522,635.
It's important to note that this calculation assumes a constant growth rate over the period, and market conditions, competition, and other factors may influence actual sales. Regularly revisiting and adjusting the business plan based on real-world performance is crucial for accurate forecasting and strategic decision-making.