Question

The average speed of blood in the aorta is 0.348 m/s, and the radius of the aorta is 1.00 cm. There are about 2.00 × 109 capillaries with an average radius of 6.26 μm. What is the approximate average speed of the blood flow in the capillaries?

Answer 1

We are given the following information

Average speed of blood in the aorta = 0.348 m/s

Radius of the aorta = 1 cm = 0.01 m

Number of capillaries = 2.00 × 10^9

Radius of capillaries = 6.26 μm

We are asked to find the average speed of the blood flow in the capillaries.

The incoming volume flow rate of blood in the aorta must be equal to the outgoing volume flow rate in the capillaries times the number of capillaries.

`Q_a=2*10^9\cdot Q_c`

The volume flow rate can be written as the product of area and speed

`A_a\cdot v_a=2*10^9\cdot A_c\cdot v_c`

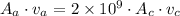
Recall that area is pi into the square of the radius.

`\begin{gathered} \pi(0.01)^2\cdot0.348=2*10^9\cdot\pi(6.26*10^(-6))^2\cdot v_c \\ (0.01)^2\cdot0.348=2*10^9\cdot(6.26*10^(-6))^2\cdot v_c \\ v_c=((0.01)^2\cdot0.348)/(2*10^9\cdot(6.26*10^(-6))^2) \\ v_c=0.44*10^(-3)\; \; (m)/(s) \end{gathered}`

Therefore, the average speed of the blood flow in the capillaries is 0.44×10^-3 m/s