Question

Need some assistance with these! Please keep them in unsimplified form!

Answer 1

`\text{(a) } a'(x)=32x^(3)+30x^(2)-6x\\\\\text{(b) } e'(x)=3\left(2x+\cos(x)\right)^2\left(2-\sin(x)\right)\\ \\\text{(c) } {f'(x)=x\left(e^((x^2-4x)\ln(3))\left(2\ln(3)x-4\ln(3)\right)\right)+3^(x^2-4x)`

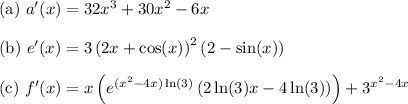
Answers are unsimplified as requested.

Explanation:

To determine the derivative of the given functions, we will apply different rules of differentiation. These rules include the power rule, the product rule, the chain rule, and the sum rule. Here’s how we will approach each function:

Given functions:

`\text{(a) } a(x)=x^2(2x+3)(4x-1)\\\\\text{(b) } e(x)=(2x+\cos(x))^3\\ \\\text{(c) } f(x) = x(3^(x^2-4x))`

`\hrulefill`

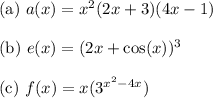
The derivatives of the given functions are as follows...

(a) The function a(x):

Expand the function to differentiate a simple polynomial.

`\Longrightarrow a(x)=x^2(2x+3)(4x-1)\\\\\\\\\Longrightarrow a(x)=x^2(8x^2-2x+12x-3)\\\\\\\\\Longrightarrow a(x)=x^2(8x^2+10x-3)\\\\\\\\\Longrightarrow a(x)=8x^4+10x^3-3x^2`

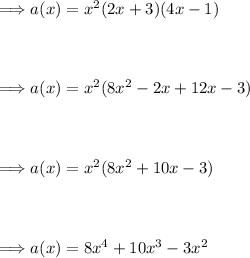
Now using the power rule we can differentiate:

`\boxed{\left\begin{array}{ccc}\text{\underline{Power Rule:}}\\\\(d)/(dx)[x^n]=nx^(n-1)\end{array}\right}`

`\displaystyle \Longrightarrow (d)/(dx)\left[a(x)=8x^4+10x^3-3x^2 \right]\\\\\\\\\Longrightarrow (d)/(dx)\left[a(x)\right]=(d)/(dx)\left[8x^4\right]+(d)/(dx)\left[10x^3\right]-(d)/(dx)\left[3x^2 \right] \\\\\\\\\therefore \boxed{\boxed{a'(x)=32x^(3)+30x^(2)-6x}}`

Thus, the derivative is found.

(b) The function e(x):

To differentiate the function e(x) we will use multiple rules. Starting with the power rule:

`\displaystyle \Longrightarrow e(x)=(2x+\cos(x))^3\\\\\\\\\Longrightarrow (d)/(dx)\left[e(x)=(2x+\cos(x))^3\right]\\\\\\\\\Longrightarrow (d)/(dx)\left[e(x)\right]=(d)/(dx)\left[(2x+\cos(x))^3\right]\\\\\\\\`

Now apply the chain rule:

`\boxed{\left\begin{array}{ccc}\text{\underline{The Chain Rule:}}\\\\(d)/(dx)\left[f(g(x))\right] =f'(g(x))\cdot g'(x)\end{array}\right}`

`\Longrightarrow e'(x)=3(2x+\cos(x))^2 \cdot (d)/(dx)\left[2x+\cos(x)\right]\\\\\\\\\Longrightarrow e'(x)=3(2x+\cos(x))^2 \cdot \left((d)/(dx)\left[2x\right]+(d)/(dx)\left[\cos(x)\right]\right)\\`

To finish, use the power rule on the 2x term and the trigometric rule for cosine:

`\boxed{\left\begin{array}{ccc}\text{\underline{Cosine Rule:}}\\\\ (d)/(dx)[\cos(x)]=-\sin(x)\end{array}\right}`

`\Longrightarrow e'(x)=3(2x+\cos(x))^2 \cdot \left(2-\sin(x)\right)\\\\\\\\\therefore \boxed{\boxed{e'(x)=3\left(2x+\cos(x)\right)^2\left(2-\sin(x)\right)}}`

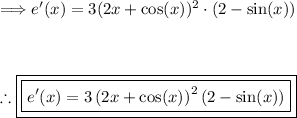
Thus, the derivative is found.

(c) The function f(x):

To differentiate the function f(x) we will use multiple rules. Starting with the product rule:

`\boxed{\left\begin{array}{ccc}\text{\underline{Product Rule:}}\\\\(d)/(dx)[f(x)g(x)]=f(x)g'(x)+g(x)f'(x) \end{array}\right }`

`\displaystyle \Longrightarrow f(x)=x\left(3^(x^2-4x)\right)\\\\\\\\\Longrightarrow (d)/(dx)\left[f(x)=x\left(3^(x^2-4x)\right)\right]\\\\\\\\\\\Longrightarrow (d)/(dx)\left[f(x)\right]=(d)/(dx)\left[x\left(3^(x^2-4x)\right)\right]\\\\\\\\\Longrightarrow f'(x)=x\left((d)/(dx)[3^(x^2-4x)]\right)+\left(x^(x^2-4x)\right)\left((d)/(dx)[x]\right)`

For the term on left apply the following exponent rule and for the term on right use the power rule:

`\boxed{\left\begin{array}{ccc}\text{\underline{Exponent Rule:}}\\\\a^b=e^(b\ln(a))\end{array}\right}`

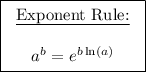
`\displaystyle \Longrightarrow f'(x)=x\left((d)/(dx)[e^((x^2-4x)\ln(3))]\right)+\left(3^(x^2-4x)\right)\left(1)`

The derivative of e^u is e^u then apply the chain rule:

`\displaystyle \Longrightarrow f'(x)=x\left(e^((x^2-4x)\ln(3)) \cdot (d)/(dx)\left[(x^2-4x)\ln(3)\right]\right)+3^(x^2-4x)`

`\displaystyle \Longrightarrow f'(x)=x\left(e^((x^2-4x)\ln(3)) \cdot (d)/(dx)\left[\ln(3)x^2-4\ln(3)x\right]\right)+3^(x^2-4x)`

Now use the power rule:

`\displaystyle \therefore \boxed{\boxed{f'(x)=x\left(e^((x^2-4x)\ln(3))\left(2\ln(3)x-4\ln(3)\right)\right)+3^(x^2-4x)}}`

Thus, the derivative is found.