To solve the question, we have to make use of the fact that
A minute hand travels 360 degrees in 60 min
From the question given, we are told that the minute hand sweep out between 9:15 and
9:35, thus
There are 20 minutes in between 9:15 and 9:35
Thus
We can get the area using the formula

Area will be
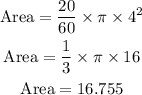
Thus, the area will be 16.76 in²