Final Answer:
The mass flux
 of the fluid through the cross-section of the cylindrical pipe is given by the formula
of the fluid through the cross-section of the cylindrical pipe is given by the formula
 , where
, where
 is the cross-sectional area of the pipe. For a cylindrical pipe,
is the cross-sectional area of the pipe. For a cylindrical pipe,
 . Therefore,
. Therefore,
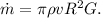
Step-by-step explanation:
In fluid dynamics, the mass flux represents the rate at which mass flows through a unit area. The formula
 expresses this relationship, where
expresses this relationship, where
 is the fluid density,
is the fluid density,
 is the velocity of the fluid, and
is the velocity of the fluid, and
 is the cross-sectional area through which the fluid is flowing.
is the cross-sectional area through which the fluid is flowing.
For a cylindrical pipe, the cross-sectional area
 is given by
is given by
 , where
, where
 is the radius of the pipe. Substituting this into the mass flux formula, we get
is the radius of the pipe. Substituting this into the mass flux formula, we get
 Additionally, the pressure gradient
Additionally, the pressure gradient
 influences the mass flux, so we multiply the formula by
influences the mass flux, so we multiply the formula by
 to incorporate this effect.
to incorporate this effect.
Therefore, the final formula for the mass flux
 in a cylindrical pipe with constant density
in a cylindrical pipe with constant density
 , viscosity
, viscosity
 , and pressure gradient
, and pressure gradient
 . This equation provides a quantitative measure of the mass flow rate through the pipe, taking into account the key factors influencing fluid dynamics in this scenario.
. This equation provides a quantitative measure of the mass flow rate through the pipe, taking into account the key factors influencing fluid dynamics in this scenario.