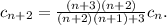Final Answer:
The coefficients
 are related by the recurrence relation
are related by the recurrence relation
Step-by-step explanation:
To find the relationship between the coefficients
 , let's substitute the power series
, let's substitute the power series
 into the given differential equation
into the given differential equation
 and solve for
and solve for
 .
.
Firstly, calculate the derivatives:
![\[ y' = \sum_(n=0)^(\infty) n c_n x^(n-1) \]](https://img.qammunity.org/2024/formulas/mathematics/college/gi1uqvnqmv5oyar5ss4kun0x0mozpgb01d.png)
![\[ y'' = \sum_(n=0)^(\infty) n(n-1) c_n x^(n-2) \]](https://img.qammunity.org/2024/formulas/mathematics/college/y4w97jtghcnssbpqjrkt1tma3k83zwnlos.png)
Now, substitute these into the differential equation:
![\[ \sum_(n=0)^(\infty) n(n-1) c_n x^(n-2) + (-x+1)\sum_(n=0)^(\infty) n c_n x^(n-1) - 3\sum_(n=0)^(\infty) c_(n) x^(n) = 0 \]](https://img.qammunity.org/2024/formulas/mathematics/college/1aux6gzuqepmlbfaqm05k84m6s11wa95zf.png)
Combine the terms and regroup:
![\[ \sum_(n=0)^(\infty) (n(n-1) c_n + n c_n - 3c_n) x^(n-2) + \sum_(n=0)^(\infty) (-x + 1)n c_n x^(n-1) = 0 \]](https://img.qammunity.org/2024/formulas/mathematics/college/ogjyoomg7f8f1vp9hvvynx0d846lis5182.png)
This yields the following recurrence relation:
![\[ n(n-1) c_n + n c_n - 3c_n = 0 \]](https://img.qammunity.org/2024/formulas/mathematics/college/8krdrnqv23apempcrrt891eelv31e9dtul.png)
Simplify this relation:
![\[ c_(n+2) = ((n+3)(n+2))/((n+2)(n+1) + 3) c_n \]](https://img.qammunity.org/2024/formulas/mathematics/college/phq6wuhewjbqb2qkuaz00z8m9jd8k7036i.png)
Thus, the coefficients
 are related by the recurrence relation
are related by the recurrence relation