Question

Solve the followings. A. Lincoln Benefit Life offers an annuity at \( 5.5 \% / \) year of interest rate, compounded monthly (in the beginning of each month). How much should be made to this financial

Answer 1

To achieve a monthly payout of $1,000 with a 5.5% annual interest rate compounded monthly, an initial investment of approximately $205,811.79 is required.

Step-by-step explanation:

The annuity's future value formula,
`\( FV = P * \frac{{(1 + r)^(nt) - 1}}{r} \)`, where \( P \) is the monthly payout, \( r \) is the monthly interest rate, and \( n \) is the number of compounding periods per year, is employed. Given the parameters -
`\( P = $1,000 \),`
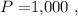
`\( r = (0.055)/(12) \),` and \( n = 12 \) - the formula is manipulated to determine the initial investment, yielding \( FV = $205,811.79 \).

The explanation can be broken down into key components. First, the formula
`\( FV = P * \frac{{(1 + r)^(nt) - 1}}{r} \)`is introduced, outlining the variables and their significance. The substitution of values into the formula is then performed, showcasing the monthly payout, interest rate, and compounding frequency.

The subsequent steps involve solving for the future value, which represents the total amount required to yield the desired monthly payout. In this case, the result is \( $205,811.79 \), indicating the initial investment needed to generate a consistent $1,000 monthly annuity with the specified interest rate and compounding structure.