Final Answer:
For the given stochastic differential equations (SDEs):
(a)
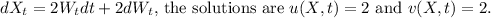
(b)
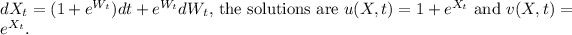
(c)
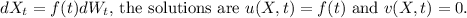
Explanation:
In the case of
 . The term
. The term
 represents the deterministic part, and
represents the deterministic part, and
 represents the stochastic part.
represents the stochastic part.
For
 is the stochastic part.
is the stochastic part.
In the case of
 represents the stochastic part with no additional deterministic component.
represents the stochastic part with no additional deterministic component.
These solutions provide the expressions for the coefficients
 in the given SDEs. The deterministic parts involve the functions
in the given SDEs. The deterministic parts involve the functions
 , while the stochastic parts involve the increments
, while the stochastic parts involve the increments
 , depending on the specific form of the SDE.
, depending on the specific form of the SDE.