Question

An economy has the following money demand function: (M/P)d=0.25Y/11/3. a. Derive an expression for the velocity of money. b. Calculate velocity if the nominal interest rate is 8 percent. c. If output Y is 1,000 units and the money supply M is $2,000, what is the price level P?

Answer 1

a) The velocity of money (V) can be expressed as
`\(V = (1)/((1)/(4) + (1)/(11/3))\).`

b) With a nominal interest rate of 8 percent, the velocity of money is approximately 3.48.

c) If output (Y) is 1,000 units and the money supply (M) is $2,000, the price level (P) is $1.50.

Step-by-step explanation:

a) The velocity of money is given by the formula
`\(V = (PY)/(M)\)`, where P is the price level, Y is the real output, and M is the money supply. From the money demand function, we have
`\((M/P)d = (0.25Y)/(11/3)\).` Solving for Y, we get
`\(Y = (11)/(12)* (M)/(P)\).` Substituting this into the velocity formula, we get
`\(V = (1)/((1)/(4) + (1)/(11/3))\).`

b) If the nominal interest rate is 8 percent, the velocity of money can be calculated using the Fisher equation: 1 + i = (1 + r)(1 +
`\pi)\)`, where i is the nominal interest rate,r is the real interest rate and
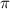`\(\pi\)` is the inflation rate. Rearranging for the real interest rate, r = i -
`\pi\)`, and substituting this into the velocity formula, we can find V.

c) With Y = 1,000 units and M = $2,000, we can use the quantity equation (MV = PY) to find the price level P. Rearranging the equation for P, we get
`\(P = (MV)/(Y)\)`. Substituting the given values, we find
`\(P = (($2,000 * 1,000))/(1,000) = $1.50\)`.

Understanding the velocity of money and its determinants is crucial in monetary economics as it relates to how quickly money circulates in the economy. The derived expressions and calculations provide insights into the factors influencing the velocity and its practical application in determining the price level.