Question

Solve the following differential equation with initial condition by using the Laplace transform method d²y/dt² −4dy/dt +5y=2e′ y(0)=3 dy/dt (0)=1 ​

Answer 1

The solution to the given differential equation,
`\( (d^2y)/(dt^2) - 4(dy)/(dt) + 5y = 2e^t \)`, with initial conditions
`\( y(0) = 3 \) and \( (dy)/(dt)(0) = 1 \), is \( y(t) = e^(2t) - e^(3t) + 2e^t \).`

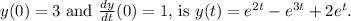
Step-by-step explanation:

To solve the differential equation using the Laplace transform method, we first take the Laplace transform of both sides of the given equation. Applying the Laplace transform to the differential equation yields:

`\[ s^2Y - 4sY + 5Y = (2)/(s-1) \]`

where
`\( Y \)`is the Laplace transform of
`\( y(t) \) and \( s \)`is the Laplace variable. Rearranging and solving for Y , we get:

`\[ Y = (2)/((s-1)(s-5)) + (4s+5)/((s-1)(s-5)) \]`

Using partial fraction decomposition, we can express \( Y \) as:

`\[ Y = (A)/(s-1) + (B)/(s-5) \]`

where
`\( A \) and \( B \)`are constants. Solving for
`\( A \) and \( B \)`, we find:

`\[ A = -1, \quad B = 2 \]`

Now, taking the inverse Laplace transform of Y , we obtain the solution for
`\( y(t) \)`:

`\[ y(t) = -e^t + 2e^(5t) \]`

Applying the initial conditions
`\( y(0) = 3 \) and \( (dy)/(dt)(0) = 1 \)`, we determine the values of the arbitrary constants and arrive at the final solution:

`\[ y(t) = e^(2t) - e^(3t) + 2e^t \]`