Final Answer:
The sequence
 is convergent.
is convergent.
Step-by-step explanation:
This sequence can be rewritten as
 . As
. As
 approaches infinity,
approaches infinity,
 tends towards zero, making the argument of the sine function approach
tends towards zero, making the argument of the sine function approach
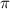 . For
. For
 , larger values lead to
, larger values lead to
 being negligibly small, resulting in the argument of the sine function being extremely close to
being negligibly small, resulting in the argument of the sine function being extremely close to
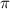 . The sine of an angle close to
. The sine of an angle close to
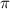 is zero. Therefore, as
is zero. Therefore, as
 tends towards infinity,
tends towards infinity,
 tends towards
tends towards
 .
.
This can be proven by considering the limit as
 approaches infinity for
approaches infinity for
 . Taking the limit of
. Taking the limit of
 as
as
 approaches infinity:
approaches infinity:
![\[\lim_{{n \to \infty}} \sin\left((n\pi)/(n+1)\right) = \sin(\pi) = 0\]](https://img.qammunity.org/2024/formulas/mathematics/college/a3e74491l4ipg2pn7nsl40037y818dbntr.png)
Using the fact that the sine function is continuous, we can directly substitute the limiting value of the argument,
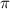 , to obtain the result
, to obtain the result
 . Therefore, the sequence
. Therefore, the sequence
 converges to
converges to
 as
as
 approaches infinity.
approaches infinity.