Final Answer:
The maximum value of y is 1/2.
Step-by-step explanation:
To find the solution y for the given initial value problem y'' + y = sin(2x) with y(0) = 0 and y'(0) = 0, we can start by solving the homogeneous equation y'' + y = 0. The characteristic equation for this homogeneous part is r² + 1 = 0, giving us
 The general solution for the homogeneous part is
The general solution for the homogeneous part is
 where A and B are constants.
where A and B are constants.
Now, for the particular solution, since the non-homogeneous term is (sin(2x)), we assume
 to be of the form
to be of the form
 . Plugging this into the original differential equation, we find that C = 0and D = 1/2, leading to the particular solution
. Plugging this into the original differential equation, we find that C = 0and D = 1/2, leading to the particular solution

The general solution is the sum of the homogeneous and particular solutions
 . Applying the initial conditions y(0) = 0 and y'(0) = 0gives A = 0 and B = 0, leaving us with the solution
. Applying the initial conditions y(0) = 0 and y'(0) = 0gives A = 0 and B = 0, leaving us with the solution
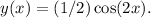
The maximum value of
 ) is 1, so the maximum value of y is 1/2.
) is 1, so the maximum value of y is 1/2.