Question

Write the equation for a parabola with vertex (-2,3) and focus (-2, 1).

Answer 1

The equation for the parabola with vertex
`\((-2,3)\)` and focus
`\((-2,1)\) is \((x+2)^2 + (y-3)^2 = 4\).`

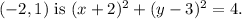
Step-by-step explanation:

To determine the equation of a parabola given its vertex and focus, it's essential to identify the key parameters. For a parabola, the standard form of the equation is
`\((x-h)^2 = 4p(y-k)\),` where
`\((h,k)\)` is the vertex, and
`\((h,k-p)\)` is the focus.

In this case, the vertex is
`\((-2,3)\), so \(h = -2\) and \(k = 3\).` The focus is given as
`\((-2,1)\),` which means
`\(p = 2\)` (the distance between the vertex and the focus). Substituting these values into the standard form, we get
`\((x+2)^2 = 8(y-3)\).` Simplifying further, we obtain
`\((x+2)^2 + (y-3)^2 = 4\),`which is the equation for the parabola.

Understanding the relationship between the vertex, focus, and parameters in the standard form of a parabola equation is crucial in geometry. It allows for the precise representation of the parabolic curve. In this case, the equation
`\((x+2)^2 + (y-3)^2 = 4\)` indicates a parabola with a vertex at
`\((-2,3)\)` and a focus at
`\((-2,1)\),` with the parameter
`\(p\)`determining the focal length.

Mastering the derivation and interpretation of equations for conic sections, such as parabolas, is valuable in various mathematical and scientific fields. The equation provides a concise representation of the parabola's characteristics and aids in further analysis and problem-solving.