Question

What is the domain of the function f(x) = √(x) + 5? 1) x < 0 2) x <= 0 3) x >= 0 4) all real numbers except x = 0 5) x > 0

Answer 1

The domain of the function
`\( f(x) = √(x) + 5 \)` is
`\( x \geq 0 \).`

Step-by-step explanation:

The given function
`\( f(x) = √(x) + 5 \)` involves the square root of
`\( x \)`, and square roots are defined only for non-negative values of
`\( x \)` since the square root of a negative number is not a real number. Therefore, the expression under the square root,
`\( x \)`, must be greater than or equal to zero for the function to be defined. Mathematically, this is represented as
`\( x \geq 0 \).`

To understand this condition intuitively, consider that taking the square root of a negative number would involve the square root of a negative one, denoted as
`\( √(-1) \)`, which is not a real number in the context of basic algebra. Hence, for the given function
`\( f(x) = √(x) + 5 \)` to have a real value,
`\( x \)` must be non-negative.

In conclusion, the domain of the function is
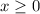`\( x \geq 0 \)`, ensuring that the square root is always taken of a non-negative value. This understanding aligns with the principles of mathematical operations, ensuring the function is well-defined for all valid inputs.