Question

Describe the dilation of g(x) = {(x) as it relates to the graph of the parent function, f(x) = x. (Lesson 4-4) ?

Answer 1

The dilation of
`\( g(x) = \{x\} \)` with respect to the parent function
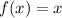`\( f(x) = x \)`involves a horizontal stretch by a factor of
`\( k \)` where
`\( k \)` is a constant greater than 1.

Step-by-step explanation:

The dilation of a function refers to a transformation that alters the size of the graph while maintaining its shape. In the context of
`\( g(x) = \{x\} \)` and the parent function
`\( f(x) = x \),` the dilation occurs horizontally. The expression
`\( g(x) = \{x\} \)` implies that the values of
`\( x \)` are enclosed in braces, indicating that
`\( g(x) \)` takes on the fractional part of
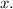`\( x \).` To understand the dilation, consider the graph of
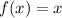`\( f(x) = x \)` as the parent function.

When
`\( g(x) \)` is dilated horizontally by a factor of
`\( k \)`, it means that the x-values in
`\( g(x) \)` are stretched or compressed. If
`\( k > 1 \)`, there is a horizontal stretch, and if
`\( 0 < k < 1 \)`, there is a horizontal compression. The function
`\( g(x) = \{x\} \)` specifically involves a horizontal stretch, implying that the fractional part of
`\( x \)` is elongated. Mathematically, this is represented as
`\( g(x) = \{kx\} \)`, where
`\( k \)` is the dilation factor. The effect is a broader graph compared to the parent function
`\( f(x) = x \).`

Understanding the concept of dilation in this context is crucial for interpreting and visualizing the changes in the graph of
`\( g(x) = \{x\} \)`concerning the parent function
`\( f(x) = x \).`It provides insight into how the function behaves as it undergoes a horizontal stretch, influencing the positioning and spacing of points along the x-axis.