Final Answer:
The difference quotient for the line
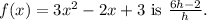
Step-by-step explanation:
To find the difference quotient, we use the formula
 . First, let's calculate ( f(x+h)) and ( f(x) ):
. First, let's calculate ( f(x+h)) and ( f(x) ):
![\[ f(x+h) = 3(x+h)^2 - 2(x+h) + 3 \]](https://img.qammunity.org/2024/formulas/mathematics/high-school/hj7i4g728th0yeisiwigqwd6mnx8aftlib.png)
Expanding and simplifying:
![\[ f(x+h) = 3(x^2 + 2xh + h^2) - 2x - 2h + 3 \]](https://img.qammunity.org/2024/formulas/mathematics/high-school/tmsq8pyukdcv8291sf737g0jfcedeoeurk.png)
![\[ f(x+h) = 3x^2 + 6xh + 3h^2 - 2x - 2h + 3 \]](https://img.qammunity.org/2024/formulas/mathematics/high-school/85j2qomcwbzt3nmo4jbk9bevw2347dw4bd.png)
Now, subtracting
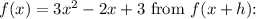
![\[ f(x+h) - f(x) = (3x^2 + 6xh + 3h^2 - 2x - 2h + 3) - (3x^2 - 2x + 3) \]](https://img.qammunity.org/2024/formulas/mathematics/high-school/8tt5c560uxfjvl3mcw1htggzlcekxhr9z4.png)
Simplifying:
![\[ f(x+h) - f(x) = 6xh + 3h^2 - 2h \]](https://img.qammunity.org/2024/formulas/mathematics/high-school/ks6t6m1iveqwz1pesy223g5x9ut1yzu6kz.png)
Now, plug this into the difference quotient formula:
![\[ (f(x+h)-f(x))/(h) = (6xh + 3h^2 - 2h)/(h) \]](https://img.qammunity.org/2024/formulas/mathematics/high-school/x9exsiw22xz8r6cobzgcbucc6qkffy4b7g.png)
Simplify further:
![\[ (6h - 2)/(h) \]](https://img.qammunity.org/2024/formulas/mathematics/high-school/nkm81z2qcrq19gimgqzx0oclvh1rkhogcu.png)
So, the difference quotient for the given line is
 This represents the average rate of change of the function ( f(x) ) with respect to ( x ) over a small interval ( h ).
This represents the average rate of change of the function ( f(x) ) with respect to ( x ) over a small interval ( h ).