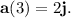Final Answer:
The equation for the path of the particle is
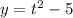 . At t = 3, the particle's velocity vector is
. At t = 3, the particle's velocity vector is
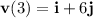 , and the acceleration vector is
, and the acceleration vector is
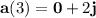 .
.
Step-by-step explanation:
To find the equation for the path of the particle, we use the position vector
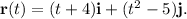 The y-coordinate of this vector is
The y-coordinate of this vector is
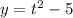 , giving us the equation for the path of the particle.
, giving us the equation for the path of the particle.
To find the velocity vector, we take the derivative of the position vector with respect to time t. The velocity vector
 is given by
is given by
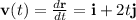 . At t = 3, the velocity vector is
. At t = 3, the velocity vector is
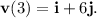
Similarly, to find the acceleration vector, we take the derivative of the velocity vector with respect to time. The acceleration vector
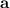 (t) is given by
(t) is given by
 ). At \(t = 3\), the acceleration vector is
). At \(t = 3\), the acceleration vector is
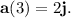
In summary, the equation for the path of the particle is
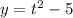 , and at
, and at
 , the particle's velocity vector is
, the particle's velocity vector is
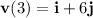 , and the acceleration vector is
, and the acceleration vector is