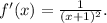Final answer:
The derivative of the function y = x/(x+1) is found using the quotient rule, resulting in the derivative
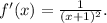
Step-by-step explanation:
To find the derivative of the function
 , we use the quotient rule which states that the derivative of a quotient of two functions is:
, we use the quotient rule which states that the derivative of a quotient of two functions is:
![f'(x) = (u'(x)v(x) - u(x)v'(x))/([v(x)]^2)](https://img.qammunity.org/2024/formulas/mathematics/high-school/mh5y914r60ukbf8szmf4woexggm91yhhi1.png)
Let u(x) = x and v(x) = x + 1. Thus, u'(x) = 1 and v'(x) = 1. Applying the quotient rule:
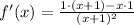
Simplifying the numerator:
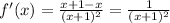
Therefore, the derivative of
 is
is