Final Answer:
The given function
 represents a cubic function with a horizontal shift to the left by 3 units and a vertical shift downward by 1 unit compared to the standard cubic function
represents a cubic function with a horizontal shift to the left by 3 units and a vertical shift downward by 1 unit compared to the standard cubic function
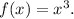
Step-by-step explanation:
The general form of a cubic function is
 which has a single stationary point (inflection point) at the origin (0, 0). In this case, the given function
which has a single stationary point (inflection point) at the origin (0, 0). In this case, the given function
 indicates transformations from the standard cubic function.
indicates transformations from the standard cubic function.
The term
 inside the parentheses causes a horizontal shift to the left by 3 units. This means that the inflection point of the cubic function is moved from (0, 0) to (-3, 0). The term
inside the parentheses causes a horizontal shift to the left by 3 units. This means that the inflection point of the cubic function is moved from (0, 0) to (-3, 0). The term
 outside the parentheses represents a vertical shift downward by 1 unit, shifting the entire graph downward.
outside the parentheses represents a vertical shift downward by 1 unit, shifting the entire graph downward.
In summary, the function
 is obtained by taking the standard cubic function and shifting it left by 3 units and down by 1 unit. The graph of \( g(x) \) will retain the basic shape of a cubic function but will be translated in the horizontal and vertical directions.
is obtained by taking the standard cubic function and shifting it left by 3 units and down by 1 unit. The graph of \( g(x) \) will retain the basic shape of a cubic function but will be translated in the horizontal and vertical directions.