Final Answer:
(a) The joint probability distribution of X and Y is as follows:
Y=0 & Y=1 & Y=2
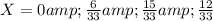
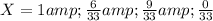
(b) To find
 , where A is the region given by
, where A is the region given by
 , sum the probabilities for the corresponding values in the joint probability distribution where
, sum the probabilities for the corresponding values in the joint probability distribution where
 . The result is
. The result is
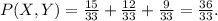
Step-by-step explanation:
(a) To determine the joint probability distribution of X and Y, we need to consider the possible combinations of X and Y. Since three cards are drawn without replacement from the deck, the probabilities depend on the outcomes of previous draws.
The joint probability distribution is given by:
Y=0 & Y=1 & Y=2
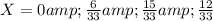
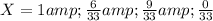
![\end{array}\]](https://img.qammunity.org/2024/formulas/mathematics/high-school/w5jl2bza895vzg4awxoa2y6kpklxuaxi1e.png)
(b) To find
 , we sum the probabilities for the values in the joint probability distribution where
, we sum the probabilities for the values in the joint probability distribution where
 . The resulting probability is
. The resulting probability is
