Solution:
Given:
The conditional statement;
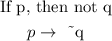
A converse statement is a result of reversing its two constituent statements.
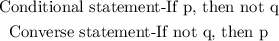
Therefore, the converse statement is: If not q, then p
The inverse statement assumes the opposite of each of the original statements.
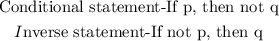
Therefore, the inverse statement is: If not p, then q
To get the contrapositive statement, we interchange the conclusion of the inverse statement.
![\begin{gathered} \text{Conditional statement-If p, then not q} \\ I\text{nverse statement-If not p, then q} \\ \\ \text{Hence, the contrapositive statement is gotten by reversing the conclusion of the inverse statement.} \\ \text{Contrapositive statement-If q, then not p} \end{gathered}]()
Therefore, the contrapositive statement is: If q, then not p