Question

A 51-cm-diameter wheel accelerates uniformly about its center from 150 rpm to 290 rpm in 4.0 s.(A) Determine it's angular acceleration. (B) Determine the radial component of the linear acceleration of a point on the edge of the wheel 1.1 s after it has started accelerating. (C) Determine the tangential component of the linear acceleration of a point on the edge of a wheel 1.1 s after it has started accelerating.

Answer 1

(A) 7/6 pi /s^2

(B) 4.145 m/s^2

(C) 119pi/200 m/s^2

Step-by-step explanation:

Part A.

The angular acceleration is given by

`\alpha=(\omega_f-\omega_i)/(\Delta t)`

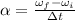
where wf is the initial angular velocity and wi is the final angular velocity and t is the time interval.

Now, we are given the angular velocity is given in rpm and we have to convert it into radians/sec .

150 rpm = 150 x 2pi / 60 min = 5 pi rad/ sec

290 rpm = 290 x 2pi / 60 min = 29/ 3 pi rad/ sec

Now we are in the position to find the angular acceleration

`\alpha=((29)/(3)\pi-5\pi)/(4s-0s)`
`\boxed{\alpha=(7)/(6)\pi\; /s^2}`

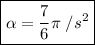
which is our answer!

Part B.

The radial acceleration is given by

`a_r=(v^2)/(R)`

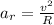
where v is the velocity of the object (moving in a circle) and R is the radius of the circle.

Now,

`v=\alpha Rt`

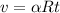
putting in the values of alpha, R and t = 1.1 s gives

`v=(7)/(6)\pi*(0.51)/(2)*1.1`
`v=1.028\; m/s`

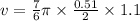
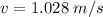
therefore,

`a_r=(v^2)/(R)=((1.028)^2)/(0.51/2)`
`\boxed{a_r=4.145/s^2}`

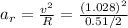
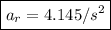
which is our answer!

Part C.

Here we have to relationship between angular and tangential acceleration:

`a=\alpha R`

where r is the radius of the circle.

Since R = 0.51/2 m, we have

`a=(7)/(6)\pi\cdot(0.51)/(2)m`

`\boxed{a=(119)/(400)\pi}`

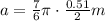
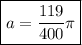
which is our answer!

Hence, to summerise

(A) 7/6 pi /s^2

(B) 4.145 m/s^2

(C) 119pi/200 m/s^2