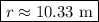Answer:
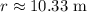
Explanation:
We can model the total volume of the figure as the sum of the volume of the cone and the volume of the cylinder:
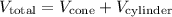
We can substitute in the the given volume formulas:
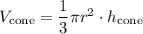
 (notice how this is equal to
(notice how this is equal to
 )
)
↓↓↓

Now, we can plug in the given volume and height values:
↓↓↓

Finally, we can solve for
 :
:
↓ factoring a
 out of both terms on the right side
out of both terms on the right side
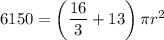
↓ executing the addition
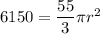
↓ dividing both sides by
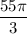
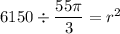
↓ rewriting dividing by a fraction as multiplying by its reciprocal

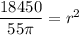
↓ taking the square root of both sides
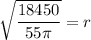
↓ evaluating using a calculator