Question

(10,7); 5x-6y=18 write an equation through the point and perpendicular to the given line

Answer 1

`\sf y =(-6)/(5)x + 19`

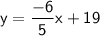
Explanation:

The product of slope of perpendicular line is (-1).

First find the slope of the given line, 5x - 6y = 18

Slope intercept of the equation: y = mx + b

• Write 5x - 6y = 18 in slope y-intercept form.
• Subtract 5x from both sides,

-6y = -5x + 18

• Divide both sides by (-6),

`\sf (-6y)/(-6)=(-5x)/(-6)+(18)/(-6)\\\\\\y = (5)/(6)x-3`

`\sf Slope = m = (5)/(6)\\\\\\\text{\bf slope of the line perpendicular to 5x - 6y = 18,} \ m_1= (-1)/(m)`

`\sf m_1= -1 / (5)/(6)\\\\\\m_1 =-1 * (6)/(5)\\\\m_1= (-6)/(5)`

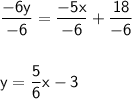
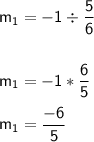
Equation of the line:

`\sf y = (-6)/(5)x + b`

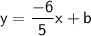
This line is passing through the point (10, 7).

`\sf 7 = (-6)/(5)*10+b\\\\7 = -6*2 + b\\\\7 = -12 + b`

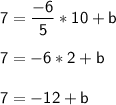
7 + 12 = b

b = 19

Equation of the line:

`\boxed{\bf y =(-6)/(5)x+19}`