Answer:
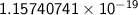
Explanation:
Let's evaluate the expression using the properties of exponents:
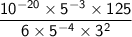
Apply the properties of exponents:
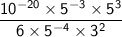
Combine the terms with the same base:
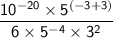
Simplify the exponents:
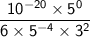
Anything raised to the power of 0 is 1:
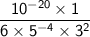
Simplify further:
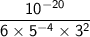
Apply the properties of exponents to the denominator:
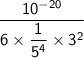
Simplify:
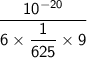
Combine terms:
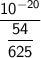
Invert and multiply:
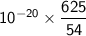
Simplify further:
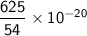
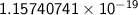
So, the simplified expression is
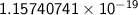 .
.