Question

For a given geometric sequence, the 6th term is -11/8, the 10th term is -22. What is the 14th term?

asked Oct 11, 2024 60.9k views

2 Answers

Laerion · Answer 1 · 2024-10-13T01:16:05+0000

Answer:

a₁₄ = -352

Explanation:

A geometric sequence is a sequence of numbers in which each term is found by multiplying the previous term by a constant factor called the common ratio (r).

The general formula for the nth term of a geometric sequence is:

a_n=ar^(n-1)

where:

is the nth term.
a is the first term.
r is the common ratio.
n is the position of the term

Given:

First, find the common ratio (r) by dividing the 10th term by the 6th term:

$\begin{aligned}(a_(10))/(a_6)=(ar^9)/(ar^5)&=(-22)/(-(11)/(8))\\\\(r^9)/(r^5)&=-22\cdot \left(-(8)/(11)\right)\\\\r^4&=16\\\\r&=\sqrt[4]{16}\\\\r&=2\end{aligned}$

Substitute r = 2 into the equation for a₁₀ and solve for a:

$\begin{aligned}a(2)^9&=-22\\\\512a&=-22\\\\a&=-(22)/(512)\\\\a&=-(11)/(256)\end{aligned}$

Therefore, the formula for the nth term of the given geometric sequence is:

$a_n=\left(-(11)/(256)\right)\cdot 2^(n-1)$

To find the 14th term, substitute n = 14 into the nth term formula:

$a_(14)=\left(-(11)/(256)\right)\cdot 2^(14-1)$

$a_(14)=\left(-(11)/(256)\right)\cdot 2^(13)$

$a_(14)=\left(-(11)/(256)\right)\cdot 8192$

a_(14)=-(90112)/(256)

a_(14)=-352

Therefore, the 14th term of the given geometric sequence is -352.

Tatigo · Answer 2 · 2024-10-15T07:28:29+0000

Answer:

$\sf a_(14) = -352$

Explanation:

In a geometric sequence, each term is found by multiplying the previous term by a common ratio (denoted as
$\sf r$ ).

Let's denote the first term of the sequence as
$\sf a$ , and the common ratio as
$\sf r$ . The general formula for the
$\sf n$ -th term of a geometric sequence is given by:

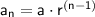
$\sf a_n = a \cdot r^((n-1))$

Given that the 6th term is
$\sf -(11)/(8)$ , we can express this as:

$\sf a_6 = a \cdot r^((6-1)) = -(11)/(8)$

Similarly, for the 10th term:

$\sf a_(10) = a \cdot r^((10-1)) = -22$

Now, we can form two equations with these pieces of information:

$\sf a \cdot r^5 = -(11)/(8)$
$\sf a \cdot r^9 = -22$

Divide the second equation by the first equation to eliminate
$\sf a$ :

$\sf (a \cdot r^9)/(a \cdot r^5) = (-22)/(-(11)/(8))$

Simplify:

$\sf r^4 = 16$

Now, solve for
$\sf r$ :

$\sf r = \sqrt[4]{16} = 2$

Now that we have the common ratio (
$\sf r = 2$ ), we can find the 14th term using the formula:

$\sf a_(14) = a \cdot r^((14-1))$

However, we need to find the value of
$\sf a$ . To do this, substitute the value of
$\sf r$ back into one of the equations, for example, the first one:

$\sf a \cdot r^5 = -(11)/(8)$

$\sf a \cdot 2^5 = -(11)/(8)$