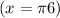Question

(π/2 -e/3)^(ln(-2cosx) ≥11[0;2π] Please solve this​ a) ( x = {pi}{2} ) b) ( x = {pi}{3} ) c) ( x = {pi}{4} ) d) ( x = {pi}{6} )

Answer 1

The solution of the inequality
`(\pi /2-e/3) ^((ln(-2cosx))\geq 11[0;2\pi]` is x ∈ (π/2, 3π/2)

None of the given options is correct

Step-by-step explanation:

The given inequality is:

`(\pi /2-e/3) ^((ln(-2cosx))\geq 11[0;2\pi]`

To solve this inequality, we need to follow these steps:

Step 1: Take the natural logarithm on both sides of the inequality.

`ln(( \pi /2 - e/3) ^((ln(-2cosx))) ) \geq ln(11)`

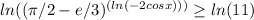
Step 2: Use the logarithm properties to simplify the left side of the inequality.

`ln(( \pi /2 - e/3) ^((ln(-2cosx)))) = (ln(-2cosx))(ln( \pi /2 - e/3))`

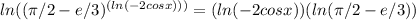
Step 3: Now, the inequality becomes:

`(ln(-2cosx))(ln( \pi /2 - e/3)) \geq ln(11)`

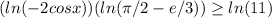
Step 4: We need to solve each part of the inequality separately.

For the first part, ln(-2cosx), the natural logarithm of a negative number is undefined. Therefore, we need to find the values of x for which -2cosx > 0.

Since the cosine function is positive in the first and second quadrants, we have:

0 < x < π/2 and π < x < 3π/2

For the second part, ln(π/2 - e/3), we need to find the values of x for which π/2 - e/3 > 0.

Solving the inequality, we get:

π/2 > e/3

3π/2 > e

So, the values of x that satisfy
`ln( \pi /2 - e/3) > ln(11)` are:

π/2 < x < 3π/2

Step 5: Now, let's find the values of x that satisfy both parts of the inequality.

Combining the results from step 4, we have:

`\pi /2 < x < 3\pi /2`

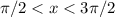
Therefore, the correct answer is: x ∈ (π/2, 3π/2)

So, none of the given options is correct

Your question is incomplete, but most probably the full question was:

`(\pi /2-e/3) ^((ln(-2cosx))\geq 11[0;2\pi]`

Please solve this​

a)
`( x = \pi2} )`

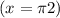
b)
`( x = \pi {3} )`

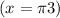
c)
`( x = \pi {4} )`

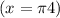
d)
`( x = \pi {6} )`