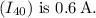(a) The current in the 25 Ω resistor

(b) The potential drop across the parallel resistors
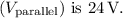
(c) The potential drop across the 25 Ω resistor
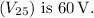
(d) The current in the 60 Ω resistor

(e) The current in the 40 Ω resistor
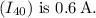
How did we get the values?
Find the equivalent resistance for the parallel resistors
 :
:
![\[ \frac{1}{R_{\text{parallel}}} = (1)/(40) + (1)/(60) + (1)/(120) \]](https://img.qammunity.org/2024/formulas/physics/high-school/wkz57jqzsej7su6fxcbfqti6n7l4pquo7d.png)
Calculating this gives:
![\[ \frac{1}{R_{\text{parallel}}} = (1)/(40) + (1)/(60) + (1)/(120) \]](https://img.qammunity.org/2024/formulas/physics/high-school/wkz57jqzsej7su6fxcbfqti6n7l4pquo7d.png)
![\[ \frac{1}{R_{\text{parallel}}} = (6 + 4 + 2)/(120) \]](https://img.qammunity.org/2024/formulas/physics/high-school/y8t8vtlqwcdl51qhcn3t77xe91j32rmf9b.png)
![\[ \frac{1}{R_{\text{parallel}}} = (12)/(120) \]](https://img.qammunity.org/2024/formulas/physics/high-school/ut1wgqp8lgnm7u2nbihl884t99he2ifqbz.png)
![\[ R_{\text{parallel}} = (120)/(12) = 10 \, \Omega \]](https://img.qammunity.org/2024/formulas/physics/high-school/bbde40owlt0zl27frfskfdh8uex0fhbl2l.png)
Find the total resistance
 for the circuit:
for the circuit:
![\[ R_{\text{total}} = R_{\text{parallel}} + R_4 + R_5 = 10 + 15 + 25 = 50 \, \Omega \]](https://img.qammunity.org/2024/formulas/physics/high-school/fxpj099lybow7x7k70mtbs8mh4ed4d00z8.png)
Find the current in the circuit
 using Ohm's Law:
using Ohm's Law:
![\[ I_{\text{total}} = \frac{V}{R_{\text{total}}} = (120)/(50) = 2.4 \, \text{A} \]](https://img.qammunity.org/2024/formulas/physics/high-school/919a55jhhyanla7wfqd1yrhw4gke77pqmo.png)
Find the potential drop across the parallel resistors
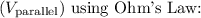
![\[ V_{\text{parallel}} = I_{\text{total}} \cdot R_{\text{parallel}} = 2.4 \cdot 10 = 24 \, \text{V} \]](https://img.qammunity.org/2024/formulas/physics/high-school/4a5mzyo04clod0k8kg684hffwb2rm3s4p1.png)
Find the potential drop across the 25 Ω resistor
 using Ohm's Law:
using Ohm's Law:
![\[ V_(25) = I_{\text{total}} \cdot R_5 = 2.4 \cdot 25 = 60 \, \text{V} \]](https://img.qammunity.org/2024/formulas/physics/high-school/8p360ljoln78eb0jh9wnltng1o7zpwm47m.png)
Find the current in the 25 Ω resistor
 using Ohm's Law:
using Ohm's Law:
![\[ I_(25) = (V_(25))/(R_5) = (60)/(25) = 2.4 \, \text{A} \]](https://img.qammunity.org/2024/formulas/physics/high-school/zdzlsfv9rrwgvrckz7u5c4hy6x2r3p2rjw.png)
Find the current in the 60 Ω resistor
 using Ohm's Law:
using Ohm's Law:
![\[ I_(60) = \frac{V_{\text{parallel}}}{R_2} = (24)/(60) = 0.4 \, \text{A} \]](https://img.qammunity.org/2024/formulas/physics/high-school/ydku5hgp5e0zy14bd7y4es1urhd0rb9juj.png)
Find the current in the 40 Ω resistor
 using Ohm's Law:
using Ohm's Law:
![\[ I_(40) = \frac{V_{\text{parallel}}}{R_1} \\= (24)/(40) \\= 0.6 \, \text{A} \]](https://img.qammunity.org/2024/formulas/physics/high-school/aejbcphxqd6u412q2ghv8m7syurp3nos5f.png)
Consequently,
(a) The current in the 25 Ω resistor

(b) The potential drop across the parallel resistors
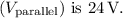
(c) The potential drop across the 25 Ω resistor
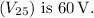
(d) The current in the 60 Ω resistor

(e) The current in the 40 Ω resistor