Answer:
1 second
Step-by-step explanation:
The equation that models the path of the ball is given below:
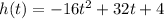
To determine how long it takes the ball takes to reach its maximum height, we find the equation of the line of symmetry.
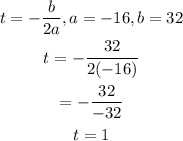
Thus, we see that it takes the ball 1 second to reach its maximum height.