Question

What is the size of angle 0 in the triangle below? Give your answer to the nearest degree.

Answer 1

The required proof is given below . And the Value of the marked angle to the nearest degree is 37°

1.)

Prove to show that the cosine rule can be arranged as :

• Cos A = (b² + c² - a²) / 2bc

Using the cosine rule which is ;

a² = b² + c² - 2bcCosA _____(1)

from (1) , we can make CosA the subject of the formula;

Add 2bcCosA to both sides

a² + 2bcCosA = b² + c²

subtract a² from both sides

2bcCosA = b² + c² - a²

divide both sides by 2bc to isolate CosA

CosA = (b² + c² - a²)/2bc ; Hence, the proof

2.)

Using the cosine formula ;

• Cos A = (b² + c² - a²) / 2bc

Inputting the values into the formula ;

Cosθ = (26² + 14² - 17²) /(2×26×14)

Cosθ = 583/728

Cosθ = 0.800

Taking the cosine inverse

θ =
`Cos^(-1) 0.8 = 36.87`

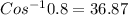
Hence, the value of the marked angle is 36.87°