Question

PRE CALC QUESTION!!!
just need answers

Answer 1

`\begin{array}\cline{1-4}&\sf Compounding\;Option&n\;\sf Value&\sf Result\\\cline{1-4}\sf (a)&\sf Annually&n=1&\$23,980.18\\\cline{1-4}\sf (b)&\sf Quarterly&n=4&\$24,087.45\\\cline{1-4}\sf (c)&\sf Monthly&n=12&\$24,111.86\\\cline{1-4}\sf (d)&\sf Daily&n=365&\$24,123.74\\\cline{1-4}\sf (e)&\sf Continuously&\sf Not\;applicable$&\$24,124.15\\\cline{1-4}\end{array}`

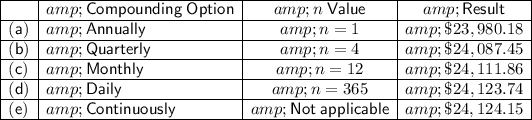
Explanation:

To calculate the balance of the account if $17,000 is invested at 3.5% interest for 10 years under different compounding options, we can use the compound interest formula:

`\boxed{\begin{array}{l}\underline{\textsf{Compound Interest Formula}}\\\\A=P\left(1+(r)/(n)\right)^(nt)\\\\\textsf{where:}\\\phantom{ww}\bullet\;\;\textsf{$A$ is the final amount.}\\\phantom{ww}\bullet\;\;\textsf{$P$ is the principal amount.}\\\phantom{ww}\bullet\;\;\textsf{$r$ is the interest rate (in decimal form).}\\\phantom{ww}\bullet\;\;\textsf{$n$ is the number of times interest is applied per year.}\\\phantom{ww}\bullet\;\;\textsf{$t$ is the time (in years).}\end{array}}`

In this case:

• P = $17,000
• r = 3.5% = 0.035
• t = 10 years

Substituting these values into the formula gives:

`A=17000\left(1+(0.035)/(n)\right)^(10n)`

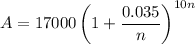
Part (a)

When interest is applied annually, substitute n = 1 into the formula:

`A=17000\left(1+(0.035)/(1)\right)^(10\cdot 1)`

`A=17000\left(1.035}\right)^(10)`

`A=23980.178930559...`

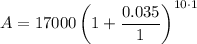
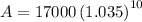
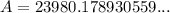
Therefore, the account balance is $23,980.18 when the interest is compounded annually (rounded to the nearest cent).

Part (b)

When interest is applied quarterly, substitute n = 4 into the formula:

`A=17000\left(1+(0.035)/(4)\right)^(10\cdot 4)`

`A=17000\left(1.00875}\right)^(40)`

`A=24087.450244829...`

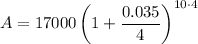
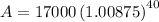
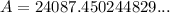
Therefore, the account balance is $24,087.45 when the interest is compounded quarterly (rounded to the nearest cent).

Part (c)

When interest is applied monthly, substitute n = 12 into the formula:

`A=17000\left(1+(0.035)/(12)\right)^(10\cdot 12)`

`A=17000\left(1.00291666...\right)^(120)`

`A=24111.86197887...`

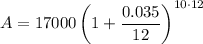
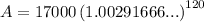
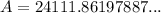
Therefore, the account balance is $24,111.86 when the interest is compounded monthly (rounded to the nearest cent).

Part (d)

When interest is applied daily, substitute n = 365 into the formula:

`A=17000\left(1+(0.035)/(365)\right)^(10\cdot 365)`

`A=17000\left(1.000095890...\right)^(3650)`

`A=24123.7435323...`

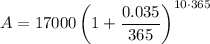
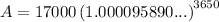
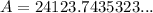
Therefore, the account balance is $24,123.74 when the interest is compounded monthly (rounded to the nearest cent).

Part (e)

To calculate the account balance when the interest is compounded continuously, we can use the following formula:

`\boxed{\begin{minipage}{8.5 cm}\underline{Continuous Compounding Interest Formula}\\\\$ A=Pe^(rt)$\\\\where:\\\\ \phantom{ww}$\bullet$ $A =$ final amount \\\phantom{ww}$\bullet$ $P =$ principal amount \\\phantom{ww}$\bullet$ $e =$ Euler's number (constant) \\\phantom{ww}$\bullet$ $r =$ annual interest rate (in decimal form) \\\phantom{ww}$\bullet$ $t =$ time (in years) \\\end{minipage}}`

Therefore:

`A=17000\cdot e^(0.035 \cdot 10)`

`A=17000\cdot e^(0.35)`

`A=17000\cdot 1.419067548...`

`A=24124.148326...`

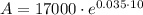
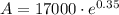
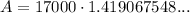
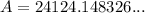
So, the account balance is $24,124.15 when the interest is compounded continuously (rounded to the nearest cent).

Completed table:

`\begin{array}l\cline{1-4}&\sf Compounding\;Option&n\;\sf Value&\sf Result\\\cline{1-4}\sf (a)&\sf Annually&n=1&\$23,980.18\\\cline{1-4}\sf (b)&\sf Quarterly&n=4&\$24,087.45\\\cline{1-4}\sf (c)&\sf Monthly&n=12&\$24,111.86\\\cline{1-4}\sf (d)&\sf Daily&n=365&\$24,123.74\\\cline{1-4}\sf (e)&\sf Continuously&\sf Not\;applicable$&\$24,124.15\\\cline{1-4}\end{array}`