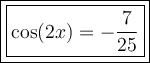Question

Use the double-angle identities to find cos (2x) if tanx = 4/3 and π < x < 3π/2

Enter an exact answer.
cos (2x) =

Answer 1

`\cos (2x)=-(7)/(25)`

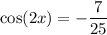
Explanation:

The tangent of an angle in a right triangle is defined as the ratio of the length of the side opposite the angle to the length of the side adjacent to the angle:

`\tan(x)=\sf (Opposide\;side)/(Adjacent\;side)`

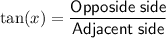
Given that tan⁡(x) = 4/3​, we can create a right triangle where the side opposite to angle x is 4, and the side adjacent to angle x is 3.

To find the length of the hypotenuse (H), use the Pythagorean Theorem:

`H=√(O^2+A^2)`

`H=√(4^2+3^2)`

`H=√(16+9)`

`H=√(25)`

`H=5`

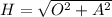
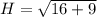
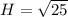
If π < x < 3π/2, then angle x is in quadrant III. In quadrant III, sin(x) and cos(x) are both negative. Therefore, using the sine and cosine trigonometric ratios, we get:

`\sin(x)=\sf -(Opposide\;side)/(Hypotenuse)=-(4)/(5)`

`\cos(x)=\sf -(Adjacent\;side)/(Hypotenuse)=-(3)/(5)`

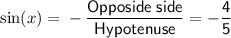
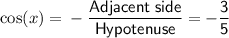
To find the value of cos(2x), we can use one of the cosine double angle identities:

`\boxed{\begin{array}{l}\underline{\textsf{Cosine Double Angle Identities}}\\\\\cos (2x)=\cos^2 x- \sin^2 x\\\\\cos(2x)=2 \cos^2 x- 1\\\\\cos (2x)=1 - 2 \sin^2 x\\\end{array}}`

Let's use cos(2x) = 2cos²(x) - 1.

Substitute the found value of cos(x) into the identity:

`\cos (2x)=2\left(-(3)/(5)\right)^2-1`

`\cos (2x)=2\left((9)/(25)\right)-1`

`\cos (2x)=(18)/(25)-1`

`\cos (2x)=(18)/(25)-(25)/(25)`

`\cos (2x)=(18-25)/(25)`

`\cos (2x)=-(7)/(25)`

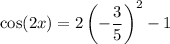
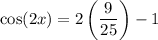
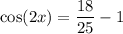
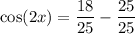
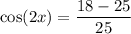
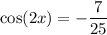
So, the exact value of cos(2x) given tan(x) = 4/3 and π < x < 3π/2 is:

`\large\boxed{\boxed{\cos (2x)=-(7)/(25)}}`