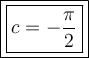Question

Find the value of c for which the function is continuous everywhere.

Answer 1

`c = -(\pi)/(2)`

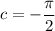
Explanation:

Given:

`f(x)=\begin{cases}c^3 + x^3,\;\;x < (\pi)/(2)\\\\c\cos(x),\;\;x\geq (\pi)/(2)\end{cases}`

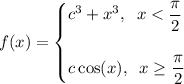
To find the value of c for which the function f(x) is continuous everywhere, we need to ensure that the function is continuous at the point x = π/2 where the two pieces of the function meet.

For a function to be continuous at a point, the following three conditions must be satisfied:

1. The function must be defined at that point.
2. The limit of the function as x approaches that point must exist.
3. The limit of the function as x approaches that point must be equal to the value of the function at that point.

Function definition

The function is defined for x < π/2 as f(x) = c³ + x³ and for x ≥ π/2 as f(x) = c cos(x). So, the function is defined at x = π/2.

Limit from the left

Evaluate the limit as x approaches π/2 from the left:

`\displaystyle \lim_{{x \to (\pi)/(2)^-}} (c^3 + x^3) = c^3 + \left((\pi)/(2)\right)^3`

Limit from the right

Evaluate the limit as x approaches π/2 from the right:

`\displaystyle \lim_{{x \to (\pi)/(2)^+}} (c\cos(x)) = c\cos\left((\pi)/(2)\right) = 0`

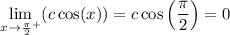
Function value at x = π/2

`f\left((\pi)/(2)\right) = c\cos\left((\pi)/(2)\right) = c * 0 = 0`

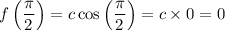
Now, for the function to be continuous at x = π/2, the limit from the left must be equal to the limit from the right, and both must be equal to the function value at that point. Therefore, we have:

`c^3 + \left((\pi)/(2)\right)^3 = 0`

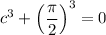
Solving for c:

`c^3 = -\left((\pi)/(2)\right)^3`

`c = -(\pi)/(2)`

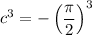
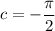
So, the value of c for which the function is continuous everywhere is:

`\large\boxed{\boxed{c = -(\pi)/(2)}}`