The magnitude of the angular acceleration is approximately
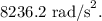
To find the magnitude of the angular acceleration, we can use the following formula:
![\[ \text{Angular acceleration (\(\alpha\))} = \frac{\text{Change in angular velocity (\(\Delta \omega\))}}{\text{Time (\(t\))}} \]](https://img.qammunity.org/2024/formulas/physics/high-school/piixse5s71u639bsw1f29fqf00eyiakt54.png)
Where:
- Change in angular velocity
 is the final angular velocity
is the final angular velocity
 minus the initial angular velocity
minus the initial angular velocity

- Time
 is the time it takes for the disk to stop.
is the time it takes for the disk to stop.
First, let's find the initial angular velocity
 and final angular velocity
and final angular velocity
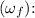
1. The disk spins at 7200 revolutions per minute (rpm), which we need to convert to radians per second (rad/s):
![\[ \omega_i = \frac{7200 \text{ rpm}}{60} * \frac{2\pi \text{ rad}}{1 \text{ min}} * \frac{1 \text{ min}}{60 \text{ s}} = 753.98 \text{ rad/s} \]](https://img.qammunity.org/2024/formulas/physics/high-school/tdvtugh8n1o293h1hsls4sehkzmukcz1d9.png)
2. To find the final angular velocity
 we need to know how many radians the disk covers in 11 revolutions. Since one revolution is equivalent to
we need to know how many radians the disk covers in 11 revolutions. Since one revolution is equivalent to
 radians, 11 revolutions will be
radians, 11 revolutions will be
 radians.
radians.
![\[ \omega_f = \frac{\text{Change in angular position}}{\text{Change in time}} = \frac{11 * 2\pi \text{ rad}}{t} \]](https://img.qammunity.org/2024/formulas/physics/high-school/vqrhre3ic9yqgkjj1bqb1t52wli2vh3f3o.png)
Now, we can calculate
 and then the angular acceleration
and then the angular acceleration
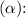
![\[ \Delta \omega = \omega_f - \omega_i = \frac{11 * 2\pi \text{ rad}}{t} - 753.98 \text{ rad/s} \]](https://img.qammunity.org/2024/formulas/physics/high-school/tdwscj28cgg39kknu547rryta653zhg93p.png)
We are given that the disk stops, so
 when it comes to rest. Therefore:
when it comes to rest. Therefore:
![\[ 0 = \frac{11 * 2\pi \text{ rad}}{t} - 753.98 \text{ rad/s} \]](https://img.qammunity.org/2024/formulas/physics/high-school/e8544b4vfd6n5kfs4i7myowdvljk2amqth.png)
Now, solve for \(t\):
![\[ t = \frac{11 * 2\pi \text{ rad}}{753.98 \text{ rad/s}} \]](https://img.qammunity.org/2024/formulas/physics/high-school/qypdten6guyo83jp49qy2zsjltdk3p7hgh.png)
Calculate
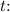
![\[ t \approx 0.0916 \text{ s} \]](https://img.qammunity.org/2024/formulas/physics/high-school/651m7r770j52p99i2w15pdkt8h84r3kwn9.png)
Now that we have the time it takes for the disk to stop, we can calculate the angular acceleration
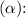
![\[ \alpha = (\Delta \omega)/(t) = \frac{-753.98 \text{ rad/s}}{0.0916 \text{ s}} \]](https://img.qammunity.org/2024/formulas/physics/high-school/d6fg7s0f84ler1mfqdlkoza33ur681fh3m.png)
Calculate
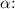
![\[ \alpha \approx -8236.2 \text{ rad/s}^2 \]](https://img.qammunity.org/2024/formulas/physics/high-school/pg74hg682qs70t7fhehml1c56507m5eiye.png)
The magnitude of the angular acceleration is approximately
 Note that the negative sign indicates deceleration or slowing down.
Note that the negative sign indicates deceleration or slowing down.