Question

10) Solve for x and graph the solution set.

Label your number line below with at least 3
numbers.
3(x + 1) ≥ 12

Answer 1

`\sf x \geq 3`

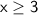
Explanation:

Let's solve the inequality
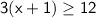`\sf 3(x + 1) \geq 12` for
`\sf x`:

`\sf 3(x + 1) \geq 12`

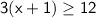
Distribute the 3 on the left side:

`\sf 3x + 3 \geq 12`

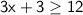
Subtract 3 from both sides to isolate the term with
`\sf x`:

`\sf 3x + 3-3 \geq 12-3`

`\sf 3x \geq 9`

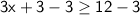
Now, divide both sides by 3 to solve for
`\sf x`:

`\sf ( 3x)/(3) \geq (9)/(3)`

`\sf x \geq 3`

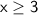
So, the solution to the inequality is
`\sf x \geq 3`.

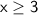Now, let's graph this on a number line:

See Attachment

On the number line, we mark the point where
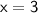`\sf x = 3` with a solid circle (indicating inclusion) and shade the region to the right because the inequality is
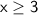`\sf x \geq 3`.