Question

Need help with finding the vertex and the Y intercept of the quadratic function and use them to graph the function for number 21

Answer 1

EXPLANATION

Given the function y=-2x^2 -12x -5

`\mathrm{The\: vertex\: of\: an\: up-down\: facing\: parabola\: of\: the\: form}\: y=ax^2+bx+c\: \mathrm{is}\: x_v=-(b)/(2a)`
`\mathrm{The\: parabola\: params\: are\colon}`
`a=-2,\: b=-12,\: c=-5`
`x_v=-(b)/(2a)`
`x_v=-(\left(-12\right))/(2\left(-2\right))`
`\mathrm{Simplify}\colon`
`x_v=-3`

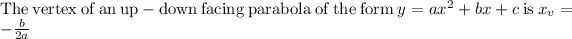
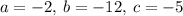
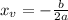
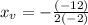
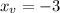
Plug in x_v=-3 to find the y_v value:

`y_v=-2\mleft(-3\mright)^2-12\mleft(-3\mright)-5`

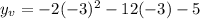
Computing the powers and multiplying terms:

`y_v=-18+36-5`

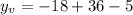
Adding and subtracting numbers:

`y_{v\text{ }}=13`

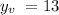
Therefore, the parabola vertex is:

(-3,13)

Now, we need to compute the y-intercept

`y\mathrm{-intercept\: is\: the\: point\: on\: the\: graph\: where\: }x=0`
`\mathrm{Apply\: rule}\: 0^a=0`
`0^2=0`
`y=-2\cdot\: 0-12\cdot\: 0-5`

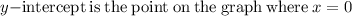
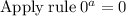
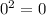
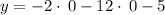
Multiplying numbers:

`y=-5`

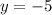
The y-intercept is at (0,-5)

In conclusion, the graph of the function is as follows: