Question

13. At what coordinate point will the graph of y=-1/2x +9 intersect with that of its inverse? Explain or sbow

how you arrived at your answers

Answer 1

(6, 6)

Explanation:

First, we should find the inverse of the function:

`f(x) =-(1)/(2)x+9`

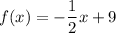
where we
`\text{let } y=f(x)`.

We can do this by listing out the operations done onto x, and inverting the order of their opposites:

f(x)

1. multiply by -1/2

2. add 9

↓↓↓

`\underline{\bold{f^(-1)}}`(x)

1. subtract 9

2. divide by -1/2

Hence,

`f^(-1)(x) = (x-9)/(-(1)/(2))`

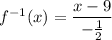
which simplifies to:

`f^(-1)(x) = -2(x-9)`

`f^(-1)(x) = -2x+18`

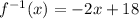
Next, we can find the point where f(x) and
`\bold{f^(-1)(x)}` intersect by equating their definitions:

`f(x) = f^(-1)(x)`

`-(1)/(2)x+9 = -2x + 18`

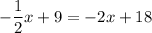
↓ adding 2x to both sides

`(3)/(2)x+9 = 18`

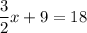
↓ subtracting 9 from both sides

`(3)/(2)x=9`

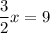
↓ multiplying both sides by 2/3

`\boxed{x = 6}`

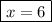
Now that we have the x-coordinate of the intersection point, we can find the y-coordinate by plugging the x-value into the function, and we can verify that our inverse function is correct by plugging it into that as well:

`f(x) =-(1)/(2)x+9`

`f(6) =-(1)/(2)(6)+9`

`f(6) =-3+9`

`\boxed{f(6)=6}`

_____________

`f^(-1)(x) = -2x+18`

`f^(-1)(x) = -2(6)+18`

`f^(-1)(x) = -12+18`

`\boxed{f^(-1)(x) = 6}`

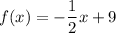
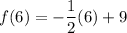
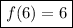
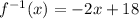
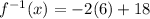
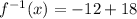
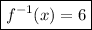
So, the point where the inverse of the function intersects with the function itself is:

(6, 6)

Further Note

The inverse of a function is also its reflection over the line y = x, so it makes sense that the point of intersection between a function and its inverse is a point on that line.