Answer:
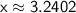
Explanation:
To solve the equation
 , we can use logarithms to simplify it.
, we can use logarithms to simplify it.
Let's take the logarithm (base 10) of both sides:
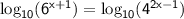
Now, we can use the logarithmic properties to simplify the exponents:
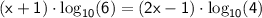
Now, let's solve for
 :
:
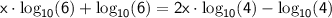
Group
 terms on one side and constants on the other:
terms on one side and constants on the other:
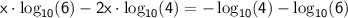
Factor out
 :
:
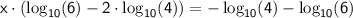
Now, solve for
 :
:
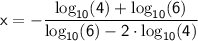
Now, use a calculator to evaluate this expression. Keep in mind that:
 and
and
 :
:
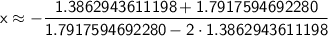
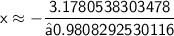
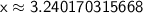
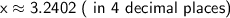
Therefore, the solution to the equation
 with four decimal places is
with four decimal places is
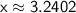 .
.