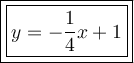Question

Write an equation for a line perpendicular to y = 4x - 4 and passing through the point (-12,4)

Answer 1

`y=-(1)/(4)x+1`

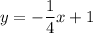
Step-by-step explanation:

The given equation y = 4x - 4 in is slope-intercept form, y = mx + b, where m is the slope and b is the y-intercept. Therefore, the slope of the given line is 4.

For any line with slope m, the slope of a line perpendicular to it is the negative reciprocal of m. So, as the given line has a slope of 4, the perpendicular line will have a slope of -1/4.

Now, substitute the found slope and point (-12, 4) into the point-slope form of a linear equation:

`\begin{aligned}y-y_1&=m(x-x_1)\\\\y-4&=-(1)/(4)(x-(-12))\\\\y-4&=-(1)/(4)(x+12)\\\\y-4&=-(1)/(4)x-3\\\\y-4+4&=-(1)/(4)x-3+4\\\\y&=-(1)/(4)x+1\end{aligned}`

So, the equation of the line perpendicular to y = 4x - 4 and passing through the point (-12, 4) is:

`\large\boxed{\boxed{y=-(1)/(4)x+1}}`

Answer 2

y = -1/4 x + 1

Step-by-step explanation:

Given line equation: y = 4x - 4 = 4(x -1)

comparing it to y = mx + c where m is the slope and c is the y-intercept

• Here the slope is 4 and y intercept -1.

We need the slope which is 4 so the line that passes perpendicularly, that line should have a slope of -1/4. As the slopes are negatively inverse for the lines that passes perpendicularly to each other.

Now equation of this line passing through (-12, 4):

• y - y1 = m(x - x1)

• y - 4 = -1/4 (x --12)

• y - 4 = -1/4 (x + 12)

• y - 4 = -1/4 x - 3

• y = -1/4 x -3 + 4

• y = -1/4 x + 1