Question

Roads in Manhattan are called streets and avenues. Streets run from east to west and avenues run from north to south.

The distance between streets is around 80 m and the distance between avenues is around 260 m, as shown below.
Point X is at the centre of the junction of 15th Street and 9th Avenue.
Point Y is at the centre of the junction of 24th Street and 5th Avenue.
Using the information above,
a) calculate the straight-line distance between point X and point Y.
b) calculate the shortest distance along the roads to get from point X to point Y.
Give your answers to the nearest metre.

Answer 1

a) 1265 m

b) 1760 m

Explanation:

Let's solve this using the figure.

In the figure attachment.

Let X be 15th street and 9th revenue.

Y be 24th street and 15th revenue.

Let the junction be O.

To calculate the straight-line distance between point X and point Y (let's call it the "as-the-crow-flies" distance), we can use the Pythagorean theorem because the streets and avenues form a grid, creating a right-angled triangle.

a) Straight-line distance between X and Y:

`\sf D = √((D_s * N_s )^2 + (D_a * N_a )^2 )`

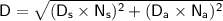
where

• 
  `\sf D` is distance
• 
  `\sf D_s` is distance between streets
• 
  `\sf N_s`is number of streets
• 
  `\sf D_a` is distance between avenues
• 
  `\sf N_a`is number of avenues

Given:

• Distance between streets: 80 m
• Distance between avenues: 260 m
• Number of streets between X and Y: 24 - 15 = 9
• Number of avenues between X and Y: 9 - 5 = 4

Now

Substitute these values in above formula and simplify it.

`\begin{aligned} Distance(D) & = √((80 * 9)^2 + (260 * 4)^2) \\\\& = √((720)^2 + (1040)^2) \\\\ & = √(518400 + 1081600) \\\\ & = √(1600000) \\\\ & = 1264.9110640673 \\\\ & \approx 1265m \textsf{( in nearest meter)}\end{aligned}`

Therefore, the straight-line distance between point X and point Y is approximately 1265 meters.

[tex]\begin{aligned} \hline \end{aligned}[/tex]

b) To calculate the shortest distance along the roads, we can use the Manhattan distance, which is the sum of the horizontal and vertical distances.

`\sf D_m = ( N_s * D_s) + (N_a * D_a )`

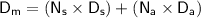
where

• 
  `\sf D_m` is Manhattan distance
• 
  `\sf D_s` is distance between streets
• 
  `\sf N_s`is number of streets
• 
  `\sf D_a` is distance between avenues
• 
  `\sf N_a`is number of avenues

Substitute these values in the above formula and simplify it.

`\begin{aligned}\textsf{Manhattan distance}(D_m) &= (9 * 80) + (4 * 260) \\\\ & = 720 + 1040 \\\\ & = 1760 \end{aligned}`

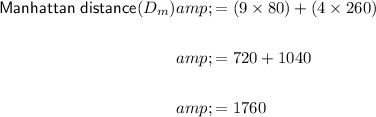
Therefore, the shortest distance along the roads from point X to point Y is approximately 1760 meters.