Question

Find the area of the sector of a circle with diameter 30 feet and an angle of 3Pi/5 radians. Round your answer to four decimal places.

Answer 1

half the diameter is the radius, so

`r=15`

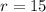
now we can calculate the total area of the circle , and then will calculate the area for the angle

`\begin{gathered} A=\pi* r^2 \\ A=\pi*15^2 \\ A=225\pi \end{gathered}`

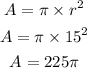
the area of the circle is 225pi, this is the corresponding area for the complete angle of the circle, therefore it is equivalent to 2pi

now we create a relation to find the area corresponding to the indicated angle

if 225pi is equal to 2pi how much is 3pi / 5

`\begin{gathered} 225\pi\longrightarrow2\pi \\ x\longrightarrow(3)/(5)\pi \end{gathered}`

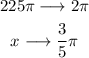
where x is the area covered by the angle

we solve ussing cross multiplication, x is equal to: multiply the values ​​that are found diagonally and make them equal

`\begin{gathered} x*2\pi=(3)/(5)\pi*225\pi \\ \end{gathered}`

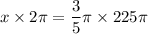
and solve for x

`\begin{gathered} x=((3)/(5)\pi*225\pi)/(2\pi) \\ \\ x=(135\pi^2)/(2\pi) \\ \\ x=67.5\pi\approx212.0575 \end{gathered}`

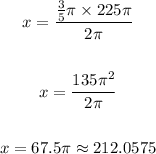
The rounded area is 212.0575 square feet